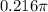To solve this exercise it is necessary to apply the kinematic equations of angular motion.
By definition we know that the displacement when there is constant angular velocity is
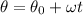
From our given data we know that,
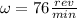
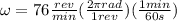
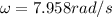
Moreover we know that
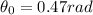
Therefore for time t=8.1s we have,
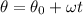
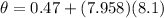
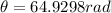
That number in revolution is:
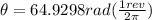
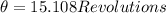
Here, we see that there are 15 complete revolutions
And 0.108 revolutions i not complete, so the tunable rotation is

Therefore the angle of the speck at a time 8.1s is