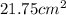Question

Air flows through a nozzle at a steady rate. At the inlet the density is 2.21 kg/m3 and the velocity is 20 m/s. At the exit, the density is 0.762 kg/m3 and the velocity is 150 m/s. If the inlet area of the nozzle is 60 cm2, determine (a) the mass flowrate through the nozzle and (b) the exit area of the nozzle.

Answer 1

To solve the problem, it is necessary to apply the concepts related to the change of mass flow for both entry and exit.

The general formula is defined by

`\dot{m}=\rho A V`

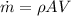
Where,

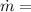`\dot{m} =` mass flow rate

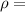`\rho =` Density

V = Velocity

Our values are divided by inlet(1) and outlet(2) by

`\rho_1 = 2.21kg/m^3`

`V_1 = 20m/s`

`A_1 = 60*10^(-4)m^2`

`\rho_2 = 0.762kg/m^3`

`V_2 = 160m/s`

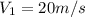
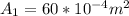
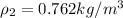
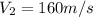
PART A) Applying the flow equation we have to

`\dot{m} = \rho_1 A_1 V_1`

`\dot{m} = (2.21)(60*10^(-4))(20)`

`\dot{m} = 0.2652kg/s`

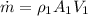
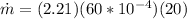
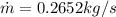
PART B) For the exit area we need to arrange the equation in function of Area, that is

`A_2 = \frac{\dot{m}}{\rho_2 V_2}`

`A_2 = (0.2652)/((0.762)(160))`

`A_2 = 2.175*10^(-3)m^2`

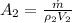
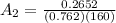
Therefore the Area at the end is
`21.75cm^2`