Question

A drainage ditch alongside a highway with a 3% grade has a rectangular cross-section of depth 4 ft and width 8 ft, and is fully packed with fragments of effective diameter of 5 inches. The void fraction within the drainage ditch is 0.42. During a rainstorm, what is the maximum capacity of the drainage ditch in gpm if the water just reaches the top of the ditch?

Answer 1

To solve the problem it is necessary to use the concepts related to frictional dissipation per unit mass, energy balance equation and Volumetric flow rate.

The frictional dissipation per unit mass is defined as

`F = (150u_0\mu L(1-\epsilon)^2)/(\rho D^2_p\epsilon^3)+1.75(u_0^2L(1-\epsilon))/(D_p\epsilon^3)`

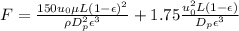
Where,

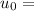`u_0 =` Superficial velocity of fluid

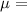`\mu =` Fluid viscoisty

`\epsilon =` Porosity

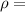`\rho =` Fluid density

L = Packed bed length

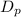`D_p` = Effective particle diameter

Through energy balance equation we have that

`\Delta(u^2)/(2)+g\Delta z+(\Delta p)/(\rho)+w+F=0`

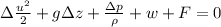
Neglect the change in velocity and pressure and the work done we have,

`g\Delta z+F = 0`

`g\Delta z+(150u_0\mu L(1-\epsilon)^2)/(\rho D^2_p\epsilon^3)+1.75(u_0^2L(1-\epsilon))/(D_p\epsilon^3)=0`

`g(\Delta z)/(L)+(150u_0\mu (1-\epsilon)^2)/(\rho D^2_p\epsilon^3)+1.75(u_0^2(1-\epsilon))/(D_p\epsilon^3)=0`

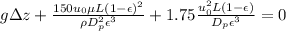
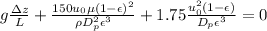
We have also that de grade is defined as

`tan\theta = (\Delta z)/(L)`

`tan\theta = 0.03`

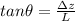
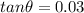
With our values and replacing at the previous equation we have,

`(32.17)(-0.03)+(150u_0(0.000672) (1-0.42)^2)/(62.3 (0.417)^2 (0.42)^3)+1.75(u_0^2(1-0.42))/((0.417)(0.42)^3)=0`

`32.85u_0^2+0.04225u_0-0.9651=0`

`u_0 = 0.171ft/s`

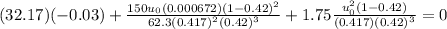
Previously with the given depth and height we have to

`A=4*8`

`A=32ft^2`

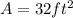
Therefore the Volumetric flow rate,

`Q=u_0A`

`Q=(0.171ft/s)(32ft^2)(60s/1min)(1gal/0.133681ft^3)`

`Q= 2456gal/min`

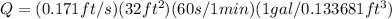
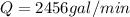
Therefore the desired volumetric flow rate is 2456gal/min