Question

A man invests a total of $9,493in two savings accounts. One account yields 9% simple interest and the other 10% simple interest. He earned a total of $930.80interest for the year. How much was invested in the 9% account?

Answer 1

$ 1850 was invested in 9% account

Solution:

Given that

Total amount invested by man in two saving accounts = $9493

Simple interest on one account =9%

Simple interest on second account = 10%

Total interest earned = $930.80

Need to determine amount invested in 9 % account.

Let assume amount invested in account where Simple Interest is 9% = x

And assume amount invested in account where Simple Interest is 10% = y

As total amount invested in two accounts is $9493

=> x + y = 9493

=> y = 9493 - x ------(1)

`\text { Simple Interest }=\frac{\text { Amount Invested } * \text {rate of interest } * \text {time}}{100}`

`\begin{array}{l}{\text { Simple interest when rate of interest is } 9 \%=(x * 9 * 1)/(100)=(9 x)/(100)} \\\\ {\text { Simple interest when rate of interest is } 10 \%=(y * 10 * 1)/(100)=(10 y)/(100)}\end{array}`

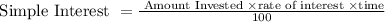
As total interest earned = $930.80

`\begin{array}{l}{\Rightarrow (9 x)/(100)+(10 y)/(100)=930.80} \\\\ {\Rightarrow 9 x+10 y=930.80 * 100} \\\\ {\Rightarrow 9 x+10 y=93080}\end{array}`

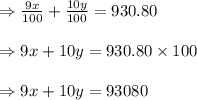
On substituting value of y from equation(1) in above equation , we get

9x + 10 (9493 – x) = 93080

=> 9x + 94930 – 10x = 93080

=> -x = 93080 – 94930

=> -x = -1850

=> x = 1850

Amount invested in account where Simple Interest is 9% = x = $1850

Hence $1850 was invested in 9% account.