Answer:
Option C. consistent independent
Explanation:
we know that
If a system has at least one solution, it is said to be consistent.
If a consistent system has exactly one solution, it is independent.
If a consistent system has an infinite number of solutions, it is dependent.
If a system has no solution, it is said to be inconsistent.
we have
 ----> equation A
----> equation A
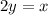 ---->
---->
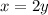 ----> equation B
----> equation B
solve the system by substitution
substitute equation B in equation A
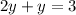
solve for y
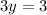
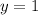
Find the value of x
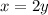 ---->
---->

The solution is the ordered pair (2,1)
The system has only one solution
therefore
The system is a consistent independent