Question

If we wanted to create a new 90% confidence interval from a different sample for the proportion of those with a two on one date while keeping the margin of error at 0.05, what would the needed sample size be? Assume you have no prior knowledge of the proportion.

Answer 1

Answer: 271

Explanation:

The formula we use to find the sample size is given by :-

`n=p(1-p)((z_(\alpha/2))/(E))^2`

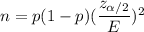
, where
`z_(\alpha/2)` is the two-tailed z-value for significance level of
`(\alpha)`

p = prior estimation of the proportion

E = Margin of error.

If prior estimation of the proportion is unknown, then we take p= 0.5 , the formula becomes

`n=0.5(1-0.5)((z_(\alpha/2))/(E))^2`

`n=0.25((z_(\alpha/2))/(E))^2`

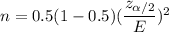
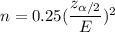
Given : Margin of error : E= 0.05

Confidence level = 90%

Significance level
`\alpha=1-0.90=0.10`

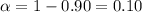
Using z-value table , Two-tailed z-value for significance level of
`0.10`

`z_(\alpha/2)=1.645`

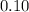
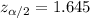
Then, the required sample size would be :

`n=0.25((1.645)/(0.05))^2`

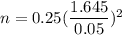
Simplify,

`n=270.6025\approx271`

Hence, the required minimum sample size =271