Answer:
angular resolution = 0.07270° = 1.269 ×
 rad
rad
greatest distance from the camera = 118.20 m = 0.118 km
Step-by-step explanation:
given data
diameter = 0.50 mm = 0.5 ×
 m
m
distance apart = 15 cm = 15×
 m
m
wavelength λ = 520 nm = 520 ×
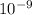 m
m
to find out
angular resolution and greatest distance from the camera
solution
first we expression here angular resolution that is
sin θ =
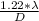 .......................1
.......................1
put here value λ is wavelength and d is diameter
we get
sin θ =
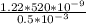
θ = 0.07270° = 1.269 ×
 rad
rad
and
distance from camera is calculate here as
θ =
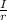 .................2
.................2
I =
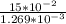
I = 118.20 m = 0.118 km