Answer:
3.636 grams of sodium bicarbonate is required.
Step-by-step explanation:
Using ideal gas equation:
PV = nRT
where,
P = Pressure of gas = 753.5 mmHg = 0.9914 atm
(
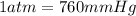 )
)
V = Volume of gas = 1.08 L
n = number of moles of gas = ?
R = Gas constant = 0.0821 L.atm/mol.K
T = Temperature of gas = 24.5 °C= 297.65 K
Putting values in above equation, we get:
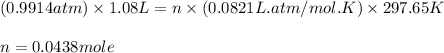
Percentage recovery of carbon dioxide gas = 49.4%
Actual moles of carbon dioxide formed: 49.4% of 0.0438 mole
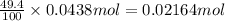
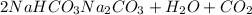
According to reaction ,1 mol is obtained from 2 moles of sodium bicarbonate.
Then 0.02164 moles f carbon dioxide will be obtained from:
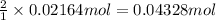
Mass of 0.04328 moles pf sodium bicarbonate:
0.04328 mol × 84 g/mol = 3.636 g
3.636 grams of sodium bicarbonate is required.