Question

A card game is played in which the player wins if a face card is drawn​ (king, queen,​ jack) from a deck of 52 cards. If the player plays 10​ times, what is the expected number of wins for the​ player? Round your answer to two decimal places.

Answer 1

The expected number of wins for the​ player is 2.31

Explanation:

No. of face cards = 12

total cards = 52

Probability of getting face card =
`\frac{\text{No. of face cards}}{\text{Total No. of cards}}`

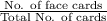
Probability of getting face card =
`(12)/(52)`

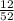
The player plays 10​ times

Formula :
`E=np`

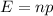
n = no. of trials = 10

p = probability of success=
`(12)/(52)`

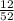
E=expected number of wins

`E=10((12)/(52))`

`E=2.307`

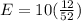
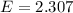
So, the expected number of wins for the​ player is 2.31