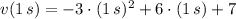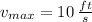Question

The position of an object along a vertical line is given by s(t) = −t3 + 3t2 + 7t + 4, where s is measured in feet and t is measured in seconds. What is the maximum velocity of the object in the time interval [0, 4]?

Answer 1

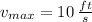`v_(max) = 10\,(ft)/(s)` at
`t = 1\,s`.

Explanation:

The velocity function is found by deriving once:

`v(t) = -3\cdot t^(2)+6\cdot t +7`

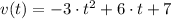
The acceleration function is determined by deriving again:

`a(t) = -6\cdot t + 6`

The critical point of the velocity function is computed by equalizing the acceleration function to zero and clearing t:

`-6\cdot t + 6 = 0`

`t = 1\,s`

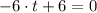
The Second Derivative Test is done by deriving the acceleration function and checking the critical point hereafter:

`\dot a (t) = -6`

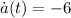
Which indicates that critical point leads to maximum velocity, which is:

`v(1\,s) = -3\cdot (1\,s)^(2) + 6\cdot (1\,s) + 7`

`v_(max) = 10\,(ft)/(s)`