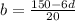Question

Marcy has 150 to buy packages of hotdogs and hamburgers for her booth at the carnival. Grocery store she found packages of hotdogs cost six packages of hamburgers cost 20

Answer 1

Part (A): The required equation will be:
`6d+20b=150`

Part (B):The required equation will be:
`d=(150-20b)/(6)`

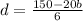
Part (C):The required equation will be:
`b=(150-6d)/(20)`

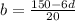
Explanation:

Consider the provided information.

Let d represents number of packages of hot dogs and b represents the number of packages of hamburgers.

Part (a)

It is given that the cost of a package of hot dogs is $6 and cost of a package of hamburger is $20.

The required equation will be:
`6d+20b=150`

Part (b) Solve the above equation for d.

Subtract 20b from both sides.

`6d=150-20b`

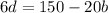
Divide 6 from both sides.

`d=(150-20b)/(6)`

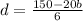
The required equation will be:
`d=(150-20b)/(6)`

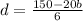
Part (c) Solve the equation for b.

Subtract 6d from both sides.

`20b=150-6d`

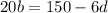
Divide 20 from both sides, we get

`b=(150-6d)/(20)`

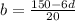
The required equation will be:
`b=(150-6d)/(20)`