Question

1 Point

What is the ratio for the volumes of two similar cylinders, given that the ratio
of their heights and radii is 2:3?
O A. 27:8
O B. 9:4
O C. 8:27
O D. 4:9

Answer 1

Option C

The ratio for the volumes of two similar cylinders is 8 : 27

Solution:

Let there are two cylinder of heights "h" and "H"

Also radius to be "r" and "R"

`\text { Volume of a cylinder }=\pi r^(2) h`

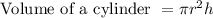
Where π = 3.14 , r is the radius and h is the height

Now the ratio of their heights and radii is 2:3 .i.e

`\frac{\mathrm{r}}{R}=\frac{\mathrm{h}}{H}=(2)/(3)`

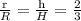
Ratio for the volumes of two cylinders

`\frac{\text {Volume of cylinder } 1}{\text {Volume of cylinder } 2}=(\pi r^(2) h)/(\pi R^(2) H)`

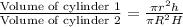
Cancelling the common terms, we get

`\frac{\text {Volume of cylinder } 1}{\text {Volume of cylinder } 2}=\left(\frac{\mathrm{r}}{R}\right)^(2) *\left(\frac{\mathrm{h}}{\mathrm{H}}\right)`

Substituting we get,

`\frac{\text {Volume of cylinder } 1}{\text {Volume of cylinder } 2}=\left((2)/(3)\right)^(2) *\left((2)/(3)\right)`

`\frac{\text {Volume of cylinder } 1}{\text {Volume of cylinder } 2}=(2 * 2 * 2)/(3 * 3 * 3)`

`\frac{\text {Volume of cylinder } 1}{\text {Volume of cylinder } 2}=(8)/(27)`

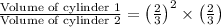
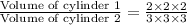
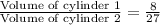
Hence, the ratio of volume of two cylinders is 8 : 27