Question

If Logx (1 / 8) = - 3 / 2, then x is equal to
A. - 4
B. 4
C. 1 / 4

Answer 1

B. 4

Explanation:

Given :

`log_x((1)/(8))=-(3)/(2)`

The logarithm function can be converted to an exponential function as

`[\log_ab=c]` can be expressed as
`[a^c=b]`

Similarly for the given expression

`log_x((1)/(8))=-(3)/(2)`

We can write,

`x^{-(3)/(2)}=(1)/(8)`

Using property of negative exponents
`[a^(-b)=(1)/(a^b)]`

`\frac{1}{x^{(3)/(2)}}=(1)/(8)`

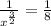
So we can write that as:

`x^{(3)/(2)}=8`

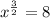
Writing the exponents in radical form as
`a^{(b)/(c)}=(\sqrt[c]{a})^b`

`(√(x))^3=8`

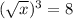
Taking cube root both sides to remove the cube.

`\sqrt[3]{(√(x))^3}=\sqrt[3]{8}`

`\sqrt x=2`

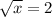
Squaring both sides to remove square root.

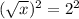
`(\sqrt x)^2=2^2`

∴
`x=4`