Question

A random sample of 25 glass sheets is obtained and their thicknesses are measured. The sample mean is x= 3.54 mm and sample standard deviation is S = 0.20 mm. Construct a 95% two-sided confidence interval for the mean glass thickness.

Answer 1

Answer: (3.46, 3.62)

Explanation:

The formula to find the confidence interval for population mean is given :-

`\overline{x}\ \pm\ t_(\alpha/2)(s)/(√(n))`

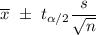
, where n = sample size.

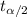`t_(\alpha/2)` = Two-tailed t-value for significance level of
`(\alpha)` and degree of freedom df= n-1.

`s` = sample standard deviation.

As per given , we have

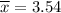`\overline{x}= 3.54` mm

s= 0.20 mm

n= 25

Significance level
`=\alpha=1-0.95=0.05`

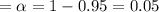
Since population standard deviation is not given , it means the given problem has t- distribution.

Two-tailed t-value for significance level of
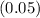`(0.05)` and degree of freedom df= 24:

`t_(\alpha/2\ ,df)=t_(0.025,\ 24)=2.0639`

95% Confidence interval for population mean:

`3.54\ \pm\ (2.0639)(0.20)/(√(25))`

`=3.54\ \pm\ (2.0639)(0.20)/(5)`

`=3.54\ \pm\ (2.0639)(0.04)`

`=3.54\ \pm\ 0.082556`

`=(3.54- 0.082556,\ 3.54+ 0.082556 )=(3.457444,\ 3.622556)\approx(3.46,\ 3.62)`

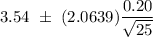
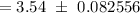
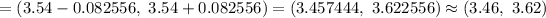
Hence, the 95% two-sided confidence interval for the mean glass thickness = (3.46, 3.62)