Question

A piston-cylinder device contains 2 lbm of refrigerant-134a at 120 psia and 100°F. The refrigerant is now cooled at constant pressure until it exists as a liquid at 50°F. Determine the entropy change of the refrigerant during this process.

Answer 1

To solve the exercise it is necessary to apply the concepts related to Entropia, that is, the measurement of the number of microstates compatible with the equilibrium macrostate, it can also be said that it measures the degree of organization of the system, or that it is the reason for an increase between internal energy versus an increase in system temperature.

Its general equation is given by

`\Delta S = m(s_2-s_1)`

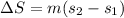
Where,

m = mass

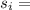`s_i =` Specific entropy (final and initial)

For our data we have that the fluid is Refrigerant 134a, with:

`m=2lbm\\P_1= 120Psi\\T_1 = 100\°F\\T_2 = 50\°F`

At the tables for super heated refrigerant 134A we have:

At
`T_1= 100\°F, P_1 = 120psia`

`s_1 = 0.22362(Btu)/(lbm.R)`

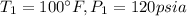
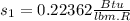
At the tables for Saturated refrigerant 134A we have

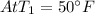`At T_1 = 50\°F`, saturated liquid

`s_2 = 0.06039(Btu)/(lbm.R)`

Therefore the total change of entropy is

`\Delta S = m(s_2-s_1)`

`\Delta S = 2*(0.06039-0.22362)`

`\Delta S = -0.32646Btu/R`

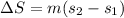
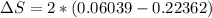
Therefore the entropy change of the refrigerant during this process is
`-0.32646Btu/R`