Question

At a distance of 11 cm from a presumably isotropic, radioactive source, a pair of students measure 65 cps (cps = counts per second). On average, how many counts per second do you expect at a distance of 20 cm? (Note that the average number of counts per second need not be an integer.)

Answer 1

To solve the problem, it is necessary the concepts related to the definition of area in a sphere, and the proportionality of the counts per second between the two distances.

The area with a certain radius and the number of counts per second is proportional to another with a greater or lesser radius, in other words,

`A_1*m=M*A_2`

`A_i =Area`

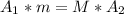
M,m = Counts per second

Our radios are given by

`r_1 = 11cm`

`R_2 = 20cm`

`m = 65cps`

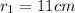
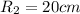
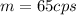
Therefore replacing we have that,

`A_1*m=M*A_2`

`4\pi r_1^2*m = M * 4\pi R_2^2 M`

`r^2*m=MR^2`

`M = (m*r^2)/(R^2)`

`M = (65*11^2)/(20^2)`

`M = 19.6625cps`

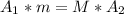
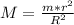
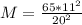
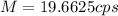
Therefore the number of counts expect at a distance of 20 cm is 19.66cps