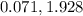Answer:
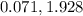
Explanation:
Downtown Store North Mall Store
Sample size n 25 20
Sample mean
 $9 $8
$9 $8
Sample standard deviation s $2 $1

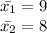

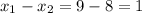
Standard error of difference of means =
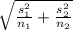
Standard error of difference of means =
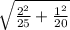
Standard error of difference of means =

Degree of freedom =

Degree of freedom =
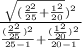
Degree of freedom =36
So, z value at 95% confidence interval and 36 degree of freedom = 2.0280
Confidence interval =
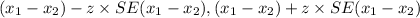
Confidence interval =

Confidence interval =
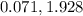
Hence Option A is true
Confidence interval is