Question

Earth's orbit around the Sun is nearly circular, with a radius of 1.50 × 10 11 m. The earth has a mass of 5.97 × 10 24 kg and takes 365.26 days to complete one orbit. What is the magnitude of its centripetal acceleration of Earth's orbital motion? m/s 2 What is the magnitude of the force necessary to cause this acceleration? N

Answer 1

Step-by-step explanation:

It is given that,

The radius of the circular path,
`r=1.5* 10^(11)\ m`

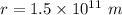
Mass of earth,
`m=5.97* 10^(24)\ kg`

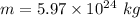
Time taken to complete one orbit,
`t = 365.26\ days =3.15* 10^7\ s`

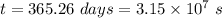
Firstly, finding the velocity of the Earth's orbital motion. It is given by :

`v=(2\pi r)/(t)`

`v=(2\pi * 1.5* 10^(11))/(3.15* 10^7)`

`v=2.99* 10^4\ m/s`

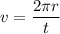
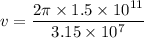
Let a is the centripetal acceleration of the Earth's orbital motion. The relation between the velocity and the acceleration is given by :

`a=(v^2)/(r)`

`a=((2.99* 10^4\ m/s)^2)/(1.5* 10^(11)\ m)`

`a=5.96* 10^(-3)\ m/s^2`

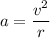
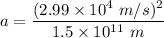
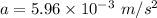
Let F is the force necessary to cause this acceleration. It is equal to the product of mass and acceleration. It is given by :

`F=m* a`

`F=5.97* 10^(24)\ kg * 5.96* 10^(-3)\ m/s^2`

`F=3.55* 10^(22)\ N`

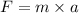
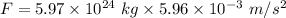
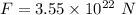
Hence, this is the required solution.