Question

A 500 gram mass is connected to a spring and undergoing uniform circular motion. The radius is at 14.5 cm and the applied centripetal force is 5.88N. The velocity of the spinning mass is measured to be 1.31 m/s. Keeping the force and mass constant the radius of the bob was increased by 1 cm. What should be the expected velocity of the spinning mass at the new radius?

Answer 1

To solve the problem it is necessary to apply the concepts related to the Centripetal Force.

By definition the centripetal force is given by

`F_c = (mv^2)/(R)`

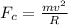
Our values are defined by

`m=0.5Kg\\F_c = 5.88N \\R = 0.145m+1cm = 0.155m\\v = 1.31m/s`

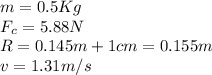
Therefore replacing in the equation we have to,

`F_c = (mv^2)/(R)`

`5.88=(0.5*v^2)/(0.155)`

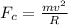
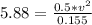
Re-arrange to find V,

`V=\sqrt{(5.88*0.155)/(0.5)}`

`V= 1.35m/s`

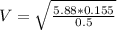
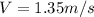
Therefore the expected velocity of the spinning mass at the new radius is 1.35m/s