Question

The collar A, having a mass of 0.75 kg is attached to a spring having a stiffness of k = 200 N/m . When rod BC rotates about the vertical axis, the collar slides outward along the smooth rod DE. The spring is unstretched when s = 0. Neglect the size of the collar. If the spring is unstretched when s = 0, determine the constant speed of the collar in order that s = 100 mm. Also, what is the normal force of the rod on the collar? Neglect the size of the collar.

Answer 1

Speed=1.633 m/s

Force= 20 N

Step-by-step explanation:

Ideally,
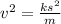`v^(2)=\frac {ks^(2)}{m}` hence
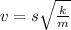`v=s\sqrt {\frac {k}{m}}` where v is the speed of collar, m is the mass of collar, k is spring constant and s is the displacement.

In this case, s=100-0=100mm=0.1m since 1 m is equivalent to 1000mm

k is given as 200 N/m and mass is 0.75 Kg

Substituting the given values

`v=0.1 m\sqrt \frac {200 N/m}{0.75 Kg}=1.632993162 m/s\approx 1.633 m/s`

Therefore, the speed is 1.633 m/s

The sum of vertical forces is given by mg where g is acceleration due to gravity and it's value taken as
`9.81 m/s^(2)`

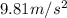
Therefore,
`F_y=0.75* 9.81=7.3575 N\approx 7.36 N`

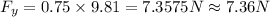
The sum of forces in normal direction is given by
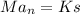`Ma_n=Ks` therefore

`Ma_n=200*0.1=20 N`

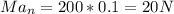
Therefore, normal force on the rod is 20 N