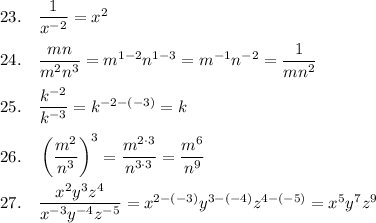Answer:
see below
Explanation:
For simplifying expressions of this sort, there are four rules of exponents that come into play;
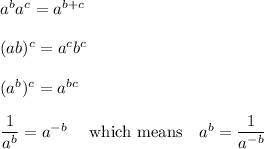
__
I find it convenient to eliminate the fractions by adding the exponents, then rewrite any negative exponents as denominator factors.