Question

4. Suppose that Peculiar Purples and Outrageous Oranges are two different and unusual types of bacteria. Both types multiply through a mechanism in which each single

bacterial cell splits into four. However, they split at different rates: Peculiar Purples split every 12 minutes, while Outrageous Oranges split every 10 minutes.
a. If the multiplication rate remains constant throughout the hour and we start with three bacterial cells of each,
after one hour, how many bacterial cells will there be of each type? Show your work and explain your answer.
b. If the multiplication rate remains constant for two hours, which type of bacteria is more abundant?
What is the difference between the numbers of the two bacterial types after two hours?
c. Write a function to model the growth of Peculiar Purples and explain what the variable and
parameters represent in the context.
d. Use your model from part (c) to determine how many Peculiar Purples there will be after three splits
(i.e., at time 36 minutes). Do you believe your model has made an accurate prediction? Why or why not?
. e.Write an expression to represent a different type of bacterial growth with an unknown initial
quantity but in which each cell splits into two at each interval of time.

Answer 1

Peculiar purples would be more abundant

Explanation:

Given that eculiar Purples and Outrageous Oranges are two different and unusual types of bacteria. Both types multiply through a mechanism in which each single bacterial cell splits into four. Time taken for one split is 12 m for I one and 10 minutes for 2nd

The function representing would be

i)
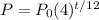`P=P_0 (4)^(t/12)` for I bacteria where t is no of minutes from start.

ii)
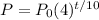`P=P_0 (4)^(t/10)` for II bacteria where t is no of minutes from start. P0 is the initial count of bacteria.

a) Here P0 =3, time t = 60 minutes.

i) I bacteria P =
`3(4)^(5) =3072`

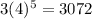
ii) II bacteria P =
`3(4)^(4) =768`

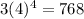
b) Since II is multiplying more we find that I type will be more abundant.

The difference in two hours would be

`3(4)^(10)- 3(4)^(8) =2949120`

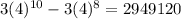
c) i)
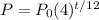`P=P_0 (4)^(t/12)` for I bacteria where t is no of minutes from start.

ii)
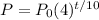`P=P_0 (4)^(t/10)` for II bacteria where t is no of minutes from start. P0 is the initial count of bacteria.

d) At time 36 minutes we have t = 36

Peculiar purples would be

`i) P=3 (4)^(36/12)=192`

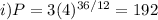
The rate may not be constant for a longer time. Hence this may not be accurate.

e) when splits into 2, we get

`P=P_o (2^t)` where P0 is initial and t = interval of time