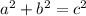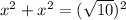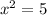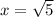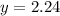Question

GEOMETRY HELP PLEASE!!! 3 questions

Answer 1

Explanation:

1. Use the Pythagorean theorem

`a^2 + b^2 = c^2`

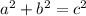
In the Pythagorean Theorem equation, a^2 + b^2 = c^2, the two sides called a and b are the legs which are the sides that form the right angle. The side called c is the hypotenuse and is the side opposite the right angle.

In this problem, the legs are x and 6.2 m. Those are called a and b.

The hypotenuse is 12.7 m which is c.

`a^2 + b^2 = c^2`

`x^2 + (6.2~m)^2 = (12.7~m)^2`

`x^2 + 38.44~m^2 = 161.29~m^2`

`x^2 = 122.85~m^2`

`x = √(122.85~m^2)`

`x = 11.1~m`

2.

`\tan A = (opp)/(adj)`

`\tan 15^\circ = (18)/(x)`

`x\tan 15^\circ = 18`

`x = (18)/(\tan 15^\circ)`

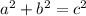
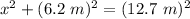
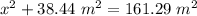
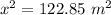
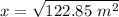
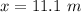
`x = 67.2`

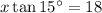
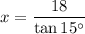
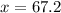
3. The triangle has a 45-deg angle and a 90-deg angle.

45 + 90 + m<3 = 180

m<3 = 45

The third angle also measures 45 deg. This is a special case called 45-45-90 triangle. The sides opposite the congruent angles are congruent, so x = y. Now we can use the Pythagorean theorem.

`a^2 + b^2 = c^2`

`x^2 + x^2 = (√(10))^2`

`2x^2 = 10`

`x^2 = 5`

`x = √(5)`

`x = 2.24`

`y = 2.24`