Question

The temperature of an incandescent lightbulb is 2500 K. Assuming the filament to be blackbody, determine the fraction of the radiant energy emitted by the filament that falls in the visible range

Answer 1

To solve this problem it is necessary the concepts related to radiant energy emitted by the bodies and their method to find it through the Blackbody radiation functions table.

From the given values we have that the temperature is 2500K and that the visible range of the electromagnetic spectrum extends from

`\lambda_1 = 0.4\mu m \leftrightarrow \lambda_2 = 0.76\mu m,`

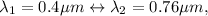
With the wavelength and temperature we can find the relationship

`\lambda * T,`then

`\lambda_1*T= (0.4\mu m)(2500K)`

`\lambda_1*T = 1000\mu m K`

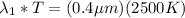
From blackbody radiation functions table (attached) we have that

`f_(\lambda_1) = 0.000321`

In the case of the second wave

`\lambda_2*T= (0.76\mu m)(2500K)`

`\lambda_2*T= 1900\mu K`

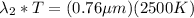
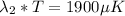
From the table,

`f_(\lambda_2) = 0.053035`

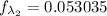
We can calculate the fraction of radian energy emitted by,

`f_(\lambda_2)-f_(\lambda_1) =  0.053035-0.0003217`

`f_(\lambda_2)-f_(\lambda_1) = 0.05272`

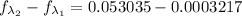
Therefore about 5% of the radiation emitted by the filament of the lightbulb falls in the visible range.