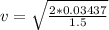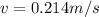Question

A 1.5 kg mass is attached to a spring with a spring constant of 110N/m. It is stretched 2.5 cm and released. What is the period of the simple harmonic motion? What is the potential energy stored in the spring prior to its release? What is the velocity of the object as it passes through the equilibrium position?

Answer 1

To solve the exercise, it is necessary the related concepts Kinetic Energy, Potential Energy and the definition of Period based on mass and elasticity constant.

PART A) So things in the case of the Period we have to be defined as

`T= 2\pi\sqrt{(m)/(k)}`

Where,

m= mass

k= Elastic constant

Replacing with our values we have that the period is,

`T = 2\pi\sqrt{(m)/(k)}`

`T= 2\pi \sqrt{(1.5)/(110N/m)}`

`T = 0.733s`

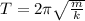
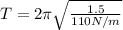
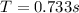
PART B) In the case of potential energy due to elasticity we have the definition of

`U=(1)/(2)kx^2`

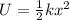
Replacing wit oru values we have

`U = (1)/(2)(110N/m)(2.5*10^(-2))^2`

`U = 0.03437J`

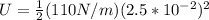
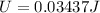
PART C) Applying the definition of kinetic energy of objects we have to

`KE = (1)/(2)mv^2`

Re-arrange to find v, we have

`v=\sqrt{(2KE)/(m)}`

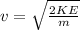
For conservation of energy we have that U (Potential energy) must be equal to KE then

`v = \sqrt{(2*0.03437)/(1.5)}`

`v = 0.214m/s`