Answer:
3 days
Step-by-step explanation:
For each isotope, we must use the integrated rate law for a first order reaction to get the rate constant k, then use that to calculate the half-life t_½.
1. Isotope A
The integrated rate law for a first-order decay is
ln(N₀/N) = kt
Data:
N₀ = 100 %
N = 10 %
t = 33 da
(a) Calculate the value of k
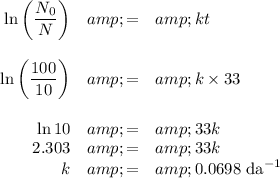
(b) Calculate the half-life

2. Isotope B
Data:
N₀ = 100 %
N = 10 %
t = 43 da
(a) Calculate the value of k
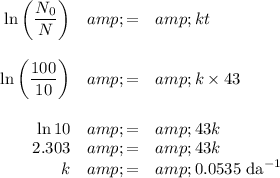
(b) Calculate the half-life
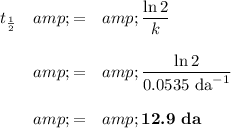
3. Calculate the difference in half-lives
Difference = 12.9 da - 9.9 da ≈ 3 da
The graphs below show the decay curves for isotopes A and B. The half-lives are approximately 10 da and 13 da, a difference of 3 da.