Answer: (16.65, 18.35)
Explanation:
By considering the given information , we have
 mm
mm
s= 4.2 mm
n= 68
Significance level

Since population standard deviation is not given ,
Formula :
Confidence interval for population mean is given :-
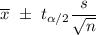
, where n = sample size.
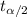 = Two-tailed t-value for significance level of
= Two-tailed t-value for significance level of
 and degree of freedom df= n-1.
and degree of freedom df= n-1.
 = sample standard deviation.
= sample standard deviation.
Two-tailed t-value for significance level of
 and degree of freedom df= 67:
and degree of freedom df= 67:
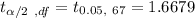
95% Confidence interval for population mean:
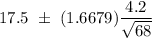
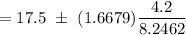
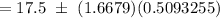
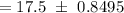
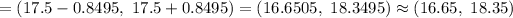
Hence, the 90% confidence interval for the population mean number of weekly customer contacts for the sales personnel. = (16.65, 18.35)