Question

What is the perimeter of the triangle?

Answer 1

21

Explanation:

By angle sum property of triangle , you get angle B = 72⁰ = angle C

Thus AB = AC = 8 cm

Perimeter = 8 + 8 + 5 =21 cm

Answer 2

The perimeter of the given triangle is 19.24 cm.

Explanation:

Here, the given triangle is a right angled triangle.

Perpendicular AB = 5 cm

Hypotenuse AC = 8 cm

Let us assume the base AB = k units

Now, by PYTHAGORAS THEOREM in a right angled triangle:

`(Base)^2 +  (Perpendicular)^2  = (Hypotenuse)^2`

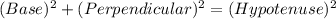
Here, in ΔABC

`(AB)^2 +  (BC)^2  = (AC)^2\\\implies (x)^2 + (5) ^2  = (8) ^2\\\\x^2 = 64 - 25 = 39\\\implies x  = √(39)  = 6.24`

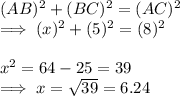
⇒ AB = 6.24 cm

Now, the PERIMETER OF A TRIANGLE = AB + BC + AC

= 6.24 cm + 8 cm + 5 cm = 19.24 cm

Hence, the perimeter of the given triangle is 19.24 cm.