Answer:
The probability that a randomly chosen child has a height of less than 51.85 inches is 0.2033
Explanation:
Mean = 54.1 inches
Standard deviation = 2.7 inches
We are supposed to find the probability that a randomly chosen child has a height of less than 51.85 inches
P(x<51.85)
Formula :

Substitute the values in the formula :

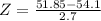

Refer the z table for p value
p value = 0.2033
Hence the probability that a randomly chosen child has a height of less than 51.85 inches is 0.2033