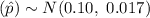Answer:
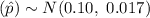
Explanation:
Sampling distribution of the sample proportion
 :
:
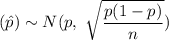
The sampling distribution of the sample proportion
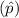 has mean =
has mean =
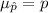 and standard deviation =
and standard deviation =
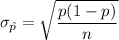 .
.
Given : The proportion of left handed people in the population is about 0.10.
i.e. p=0.10
sample size : n= 300
Then , the sampling distribution of the sample proportion
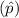 will be :-
will be :-
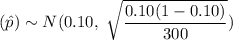
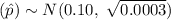
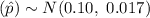 (approx)
(approx)
Hence, the sampling distribution of the sample proportion
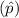 is
is