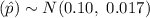Question

The proportion of left handed people in the population is about 0.10. Suppose a random sample of 300 people is observed. (a) What is the sampling distribution of the sample proportion (p-hat)

Answer 1

Answer:
`(\hat{p})\sim N(0.10,\ 0.017)`

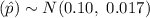
Explanation:

Sampling distribution of the sample proportion
`(\hat{p})` :

`(\hat{p})\sim N(p,\ \sqrt{(p(1-p))/(n)})`

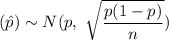
The sampling distribution of the sample proportion
`(\hat{p})` has mean =
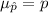`\mu_{\hat{p}}=p` and standard deviation =
`\sigma_{\hat{p}}=\sqrt{(p(1-p))/(n)}`.

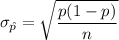Given : The proportion of left handed people in the population is about 0.10.

i.e. p=0.10

sample size : n= 300

Then , the sampling distribution of the sample proportion
`(\hat{p})` will be :-

`(\hat{p})\sim N(0.10,\ \sqrt{(0.10(1-0.10))/(300)})`

`(\hat{p})\sim N(0.10,\ √(0.0003))`

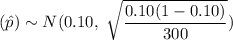
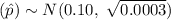
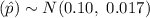`(\hat{p})\sim N(0.10,\ 0.017)` (approx)

Hence, the sampling distribution of the sample proportion
`(\hat{p})` is
`(\hat{p})\sim N(0.10,\ 0.017)`