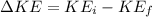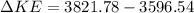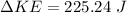Answer:
a)
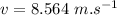
b)
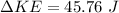
c)
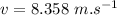
d)
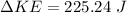
Step-by-step explanation:
Given:
mass of the player,
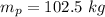
mass of the ball,
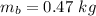
initial velocity of the player,
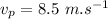
initial velocity of the ball,
a)
Case: When the player and the ball are moving in the same direction.
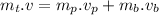
where:
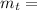 total mass after the player catches the ball
total mass after the player catches the ball
v = final velocity of the system
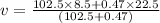
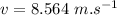
b)
Initial kinetic energy of the system:
![KE_i=(1)/(2) [m_p.v_p^2+m_b.v_b^2]](https://img.qammunity.org/2020/formulas/physics/college/m0kq32j2ip2j4aucuhlhy57ojml1p5pkss.png)
![KE_i=(1)/(2) [102.5* 8.5^2+0.47* 22.5^2]](https://img.qammunity.org/2020/formulas/physics/college/jgj5sghs6gbuu9aqijn89g73b2gj0eng1c.png)
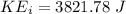
Final kinetic energy of the system:
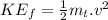
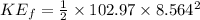
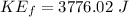
∴Change in kinetic energy
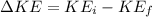
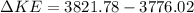
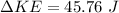
c)
Case: When the player and the ball are moving in the opposite direction.
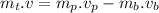
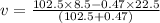
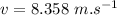
d)
Final kinetic energy in this case:
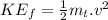
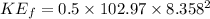
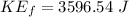
∴Change in kinetic energy: