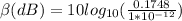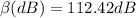Question

At the race track, one race car starts its engine with a resulting intensity level of 104.0 dB at point P. Then 6 more cars start their engines. If the other 6 cars each produce the same intensity level at point P as the first car, what is the new intensity level with all 7 cars running?

Answer 1

To solve the problem it is necessary to apply the concepts related to sound intensity. The most common approach to sound intensity measurement is to use the decibel scale:

`\beta (dB) = 10log_(10)((I)/(I_0))`

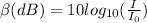
Where,

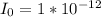`I_0 = 1*10^(-12)` is a reference intensity. It is the lowest or threshold intensity of sound a person with normal hearing can perceive at a frequency of 1000 Hz.

I = Sound intensity

Our values are given by,

`\beta = 104dB`

`\#Autos = 7`

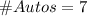
For each auto the intensity would be,

`104 = 10log(I)/(1*10^(-12))`

`10.4= log_(10) ((I)/(10^(-12)))`

`10^(10.4)*10^(-12)=I`

`I = 0.02511W/m^2`

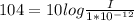
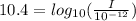
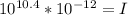
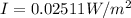
Therefore the sound intesity for the 7 autos is

`I= 7* 0.02511`

`I = 0.1748W/m^2`

The sound level for the 7 cars in dB is

`\beta (dB) = 10log_(10)((0.1748)/(1*10^(-12)))`

`\beta (dB) = 112.42dB`