Question

Suppose that a wing component on an aircraft is fabricated from an aluminum alloy that has a plane strain fracture toughness of 25 MPa (22.75 ksi). It has been determined that fracture results at a stress of 101 MPa (14650 psi) when the maximum internal crack length is 8.8 mm (0.3465 in.). For this same component and alloy, compute the stress level at which fracture will occur for a critical internal crack length of 6.3 mm (0.2480 in.).

Answer 1

stress level is 119.67 MPa

Step-by-step explanation:

given data

strain fracture toughness = 25 MPa

stress = 101 MPa

maximum internal crack length = 8.8 mm

critical internal crack length = 6.3 mm

to find out

stress level

solution

we first find here Y parameter that is

Y =
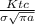`(Ktc)/(\sigma √(\pi a))` ......................1

here σ is stress level that is given and Ktc is fracture toughness and a is half of crack length so solve it

Y =
`\frac{25}{101 \sqrt{\pi (8.8*10^(-3))/(2)}}`

Y = 2.10

so now we solve stress level from equation 1

Y =
`(Ktc)/(\sigma √(\pi a))`

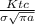
σ =
`(Ktc)/(Y √(\pi a))`

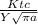
put here value

σ =
`\frac{25}{2.10 \sqrt{\pi (6.3*10^(-3))/(2)}}`

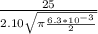
σ = 119.67 MPa