Question

Suppose you have 4 colors to color the 3 edges of an equilateral triangle. How manyways can you color the triangle if two ways are considered the same if they differby a rotation? Include a clear description of how you came to your number.

Answer 1

Here we have four colour for three sides of the triangle. So for each side we have four choices available until we have any two same by rotation.

Explanation:

Answer 2

4

Explanation:

There will be the number of ways to arrange n objects. In fact, the factorial method is used to calculate the number of ways for arranging n objects will be like this:

n! = n * (n-1)* (n-2)* (n-3) * ...*3*2*1

Another method will be to sue the binomial method or combinations:

(n r) =
`(n!)/(r!(n-r)!)`

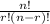
To arrange 4 colors over 3 edges, this means that:

n =
`(4!)/(3!(4-3)!)`

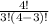
= 4

Therefore, there will be 4 ways of arranging the numbers.