Answer: y = 3
 - 2x + 2
- 2x + 2
Explanation:
The equation in standard form of a parabola is given as :
y =
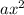 + bx + c
+ bx + c
The points given are :
( -2 , 18 ) , ( 0,2) , ( 4 , 42)
This means that :
 = -2
= -2
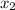 = 0
= 0
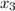 = 4
= 4
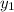 = 18
= 18
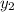 = 2
= 2
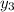 = 42
= 42
All we need do is to substitute each of this points into the equation , that is ,
 and
and
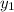 will be substituted to get an equation ,
will be substituted to get an equation ,
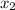 and
and
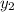 will be substituted to get an equation and
will be substituted to get an equation and
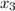 ,
,
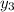 will also be substituted to get an equation also.
will also be substituted to get an equation also.
Starting with the first one , we have :
y =
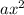 + bx + c
+ bx + c
18 = a[
 ] + b (-2) + c
] + b (-2) + c
18 = 4a - 2b + c
Therefore :
4a - 2b + c = 18 ................ equation 1
substituting the second values , we have
2 = a (0) + b ( 0) + c
2 = c
Therefore c = 2 ............... equation 2
also substituting the third values , we have
42 = a[
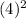 ] + b (4) + c
] + b (4) + c
42 = 16a + 4b + c
Therefore
16a + 4b + c = 42 ........... equation 3
Combining the three equations we have:
4a - 2b + c = 18 ................ equation 1
c = 2 ............... equation 2
16a + 4b + c = 42 ........... equation 3
Solving the resulting linear equations:
substitute equation 2 into equation 1 and equation 3 ,
substituting into equation 1 first we have
4a - 2b + 2 = 18
4a - 2b = 16
dividing through by 2 , we have
2a - b = 8 ............... equation 4
substituting c = 2 into equation 3 , we have
16a + 4b + c = 42
16a + 4b + 2 = 42
16a + 4b = 40
dividing through by 4 , we have
4a + b = 10 ................ equation 5
combining equation 4 and 5 , we have
2a - b = 8 ............... equation 4
4a + b = 10 ................ equation 5
Adding the two equations to eliminate b , we have
6a = 18
a = 18/6
a = 3
Substituting a = 3 into equation 4 to find the value of b , we have
2(3) - b = 8
6 - b = 8
b = 6 - 8
b = -2
Therefore :
a = 3 , b = -2 and c = 2
Substituting these values into the equation of parabola in standard form , we have
y = 3
 - 2x + 2
- 2x + 2