Question

The number of coffee shops in a certain country can be modeled by the quadratic function

f ( x )=110 x squared + 746 x + 4417,

where​ f(x) is the number of coffee shops and x is the number of years after 2000. Complete parts a and b

a. Find the number of coffee shops in

2004.

b. If the trend described by the model​ continues, predict the year after 2000 in which the number of coffee shops will be 26,500.

a. The number of coffee shops in 2004
was

 

​

Answer 1

a. 9161

b. 2011

Explanation:

The number of coffee shops in the country can be modeled as by the function: f(x) = 110x² + 746x + 4417, where f(x) is the number of coffee shops and x is the number of years after 2000.

a. Now, in 2004, the x value is (2004 - 2000) = 4.

Therefore, f(4) = 110 × 4² + 746 × 4 + 4417 = 9161

So, the number of coffee shops in 2004 is 9161.

b. If f(x) = 26500, then we have to find the value of x.

So, 110x² + 746x + 4417 = 26500

⇒ 110x² + 746x - 22083 = 0

Applying the Sridhar Achaya formula to find x,

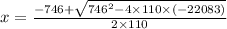`x = \frac{-746 + \sqrt{746^(2) - 4 * 110 * (-22083) } }{2 * 110}` {Neglecting the negative roots as x can not be negative}

⇒ x = 11.17 years.

If ax² + bx + c = 0, then Using the Sridhar Acharya Formula, we can write

`x = \frac{-b + \sqrt{b^(2) - 4ac } }{2a}` and
`x = \frac{-b - \sqrt{b^(2) - 4ac } }{2a}`

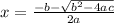
Therefore, in 2011 the number of coffee shop will be 26500.