Answer:
vf₂ = 16 m/s
Step-by-step explanation:
Theory of collisions
Linear momentum is a vector magnitude (same direction of the velocity) and its magnitude is calculated like this:
P=m*v
where
P:Linear momentum
m: mass
v:velocity
There are 3 cases of collisions : elastic, inelastic and plastic.
For the three cases the total linear momentum quantity is conserved:
P₀ = Pf Formula (1)
P₀ : Initial linear momentum quantity
Pf : final linear momentum quantity
Data
m₁ = 600 g
m₂= 200 g
v₀₁ = 8 m/s :initial velocity of m₁
v₀₂ = - 8 m/s :initial velocity of m₂ ; (-) indicates that m₂ is moving in the opposite direction to m₁
Problem development
We appy the formula (1):
We assume that at the end of the collide both masses move in the initial direction of m₁ , then vf₁ and vf₁ have a sign (+)
P₀ = Pf
m₁*v₀₁ + m₂*v₀₂ = m₁*vf₁ + m₂*vf₂
(600) *(8)+ (200)*( -8) = (600) *vf₁ + (200)*vf₂
4800 - 1600 = (600) *vf₁ + (200)*vf₂
3200 = (600) *vf₁ + (200)*vf₂ : We divide both sides of the equation by 100
32= 6*vf₁ +2*vf₂ Equation (1)
For elastic collision, the elastic restitution coefficient (e) is equal to 1 :
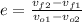
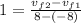
16 = vf₂ - vf₁
vf₁ = vf₂ - 16 Equation (2)
We replace Equation (2) in the Equation (1)
32= 6*vf₁ +2*vf₂
32= 6*( vf₂ - 16) +2*vf₂
32= 6*vf₂ - 96 + 2*vf₂
32 + 96= 6*vf₂ + 2*vf₂
128 = 8 *vf₂
vf₂ = 128 / 8
vf₂ = 16 m/s