To develop the problem it is necessary to apply two concepts, the first is related to the calculation of average data and the second is the Boltzmann distribution.
Boltzmann distribution is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system. It is given by
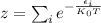
Where,
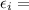 energy of that state
energy of that state
k = Boltzmann's constant
T = Temperature
With our values we have that
T= 250K



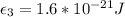
To make the calculations easier we can assume that the temperature and Boltzmann constant can be summarized as
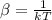

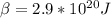
Therefore the average energy would be,
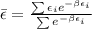
Replacing with our values we have


Therefore the average internal energy is
