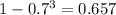Question

Thirty percent of the CFA candidates have a degree in economics. A random sample of three CFA candidates is selected. What is the probability that at least one of them has a degree in economics?

Answer 1

This is an example of a random variable that follows Bernoulli distribution.

Whenever you perform
`n` experiments, with probability
`p` of success, the provability of havin
`k`successes is

`P(X=k)=\displaystyle\binom{n}{k}p^k(1-p)^(n-k)`

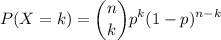
In this case, you have
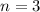`n=3` (you choose a sample of 3 candidates),
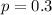`p=0.3` (30% of candidates have a degree in economics) and we want
`k` to be at least one.

One way to solve this is to consider that

`P(X\geq 1)=P(X=1)+P(X=2)+P(X=3)`

But it is much quicker to observe that

`P(X\geq 1)=1-P(X<1)=1-P(X=0)`

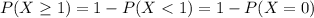
And we have

`P(X=0)=\displaystyle\binom{3}{0}0.3^0\cdot 0.7^(3)=1\cdot 1\cdot 0.7^3`

So, the probability that at least one of them has a degree in economics is

`1-0.7^3 = 0.657`