Question

What change would you expect on the rate of the SN2 reaction of 1-iodo-2-methylbutane with cyanide ion if the nucleophile concentration is halved and the alkyl halide concentration is unchanged ?

Answer 1

Rate of reaction will be half of it's initial value

Step-by-step explanation:

For the given
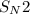`S_(N)2` reaction, the rate law is -

`Rate=k[1-iodo-2-methylbutane][CN^(-)]`

Where k is rate constant, [1-iodo-2-methylbutane] is concentration of 1-iodo-2-methylbutane and
`[CN^(-)]` is concentration of
`CN^(-)`

Here nucleophile is the
`CN^(-)` ion

Initiallly,
`(Rate)_(initial)=k* [1-iodo-2-methylbutane]_(initial)* [CN^(-)]_(initial)`

When concentration of
`CN^(-)` is halved then-

`Rate=k* [1-iodo-2-methylbutane]_(initial)* ([CN^(-)]_(initial))/(2)=((Rate)_(initial))/(2)`

So rate of reaction will be half of it's initial value