Answer:Slope=8,
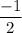 ,equation is
,equation is
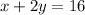 .
.
Explanation:
Y-intercept of the line is defined as y-coordinate the point where the line crosses the y-axis.
We can see from the graph that the line passes y axis at
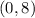
So,y intercept is

Let
 be the slope of a line which passes through
be the slope of a line which passes through
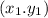 and
and
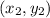
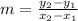
The given line passes through
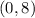 and
and
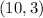
So,
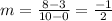 .
.
Equation of a line that passes through
 and slope
and slope
 is
is
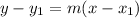 .
.
It is given that the line passes through
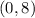
So, the equation is
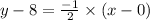
So,
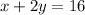 is equation of the the given line when simplified.
is equation of the the given line when simplified.