72 m is the horizontal distance the travels.
Option: C
Step-by-step explanation:
The units to express the horizontal and vertical distances are meters (m). The "horizontal" and "vertical" velocities are expressed in "meters per second" (m/s).
Horizontal distance = (initial horizontal velocity)(time)
We can now get the range x from the horizontal component of velocity
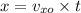 equation (1)
equation (1)
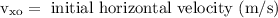
x = horizontal distance (m)
t = time (s)
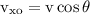
We know that, V = 37 m/s, θ = 12 degree and t = 2 seconds.
To find,
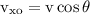
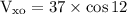
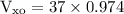
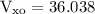
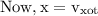
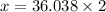
x = 72.076 m ~ 72 m
x = 72 m
The horizontal distance is 72 m.