Question

A 30-tooth gear has AGMA standard full-depth involute teeth with diametral pitch of 12. Calculate the pitch diameter, circular pitch, addendum, dedendum, tooth thickness, and clearance.

Answer 1

To develop the problem it is necessary to apply the concepts related to Pitch diameter, circular pitch, addendum, dedendum, tooth thickness, and clearance.

The pitch diameter of the gear is defined as

`d = (N)/(p_d)`

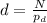
Where,

N = Number of teeth

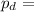`p_d =` Diametral pitch

Replacing we have

`d=frac{30}{12}\\d = 2.500`

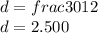
Therefore the pitch diameter of the gear is 2.500

The circular pitch of the gear is given as

`p_c = (\pi)/(p_d)\\p_c = (\pi)/(12)\\p_c = 0.2618`

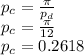
Therefore the circular pitch of the gear is 0.2618

The addendum of the gear teeth is given by

`a = (1000)/(p_d)\\a = (1000)/(12)\\a=0.0833`

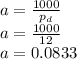
Therefore the addendum of the gear teeth is 0.0833

The dedendum of the gear teeth is gives as

`b = (1.250)/(p_d)\\b = (1.250)/(12)\\b = 0.1042`

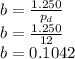
The thickness of the tooth is given by

`t=0.5p_c \\t = 0.5*0.2618\\t = 0.1309`

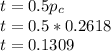
Therefore the thickness is 0.1309

Finally the clearance is given by

`c = (0.250)/(p_d)\\c = (0.250)/(12)\\c = 0.0208`

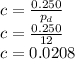
Therefore the clearance of the gear teeth is 0.028

As you can see most of the definitions are made from a theoretical aspect of defined equations for each of the parameters.