Question

The vertices of a parallelogram are J(?5, 0), K(1, 4), L(3, 1), and M(?3,?3). Find the slope of each side. Slope of JK = slope of KL = slope of LM = slope of MJ =

Answer 1

The slope of JK is 2/3.

The slope of KL is -3/2.

The slope of LM is 2/3.

The slope of MJ is -3/2.

Explanation:

Consider the provided vertices.

We can find the slope by using the value.

`Slope=m=(y_2-y_1)/(x_2-x_1)`

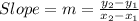
The vertices of a parallelogram are J(-5, 0), K(1, 4), L(3, 1), and M(-3,-3).

Find slope of JK by using the points J(-5, 0) and K(1, 4).

`m=(4-0)/(1-(-5))=(2)/(3)`

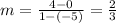
The slope of JK is 2/3.

Find slope of KL by using the points K(1, 4) and L(3, 1).

`m=(1-4)/(3-1)=(-3)/(2)`

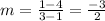
The slope of KL is -3/2.

Find slope of LM by using the points L(3, 1) and M(-3,-3).

`m=(-3-1)/(-3-3)=(2)/(3)`

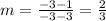
The slope of LM is 2/3.

Find slope of MJ by using the points M(-3,-3) and J(-5, 0).

`m=(0+3)/(-5+3)=(3)/(-2)`

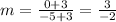
The slope of MJ is -3/2.