Question

Treasury bonds paying an 8.25% coupon rate with semiannual payments currently sell at par value. What coupon rate would they have to pay in order to sell at par if they paid their coupons annually?

Answer 1

8.42%

Step-by-step explanation:

If Bond price is equal to face value, then it means that YTM of the bond is also equal to coupon rate;

If YTM = Coupon rate, Price = Face value

Since the coupon rate = 8.25%, YTM (APR)= 8.25%

Next, find the Effective YTM or effective annual return(EAR) ;

Effective YTM or EAR =
`(1+(APR)/(m)) ^(m) -1`

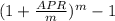
m = number of compounding periods per year; 2 in this case

EAR =
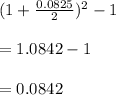`(1+(0.0825)/(2)) ^(2) -1\\ \\ = 1.0842 - 1\\ \\ =0.0842` or 8.42%

Therefore, if coupons are paid annually, the coupon yield will be equivalent to the 8.42% YTM;

Effective YTM = Coupon rate = 8.42%