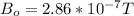Question

A light source radiates 60.0 W of single-wavelength sinusoidal light uniformly in all directions. What is the amplitude of the magnetic field of this light at a distance of 0.700 m from the bulb?

Answer 1

To solve this problem it is necessary to take into account the concepts of Intensity as a function of Power and the definition of magnetic field.

The intensity depending on the power is defined as

`I = (P)/(4\pi r^2),`

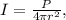
Where

P = Power

r = Radius

Replacing the values that we have,

`I = (60)/((4*\pi (0.7)^2))`

`I = 9.75 Watt/m^2`

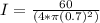
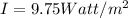
The definition of intensity tells us that,

`I = (1)/(2)(B_o^2 c)/(\mu)`

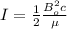
Where,

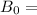`B_0 =`Magnetic field

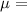`\mu =` Permeability constant

c = Speed velocity

Then replacing with our values we have,

`9.75 = (Bo^2 (3*10^8))/((4\pi*10^(-7)))`

Re-arrange to find the magnetic Field B_0

`B_o = 2.86*10^(-7) T`

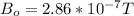
Therefore the amplitude of the magnetic field of this light is
`B_o = 2.86*10^(-7) T`