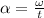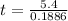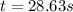Question

After fixing a flat tire on a bicycle you give the wheel a spin. Its initial angular speed was 5.40 rad/s and it rotated 12.3 revolutions before coming to rest. You may want to review what was itsaverage angular acceleration? (Consider speeding up postive andslowing down negative.)

1 rad/s2

(b) For what length of time did the wheel rotate?
2 s

Answer 1

To solve this problem it is necessary to apply the concepts related to the kinematic equations of angular motion.

By definition, acceleration can be expressed as the change in angular velocity squared over a given period of distance traveled.

`\alpha = (\omega^2)/(2\theta)`

where,

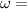`\omega =` Angular velocity

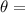`\theta =` Angular displacement.

In turn, as a function of time, we can represent it as,

`\alpha = (\omega)/(t)`

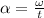
For our case we have to,

`\omega = 5.4rad/s`

`\theta = 12.3rev = 12.3rev((2\pi rad)/(1rev))=24.6\pi rad`

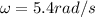
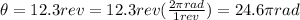
PART A) In the case of angular acceleration we have to,

`\alpha = (\omega^2)/(2\theta)`

`\alpha = ((5.4)^2)/(2*24.6\pi)`

`\alpha = 0.1886rad/s^2`

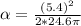
PART B) Through the definition of angular acceleration as a function of time we can calculate it,

`\alpha = (\omega)/(t)`

`t = (\omega)/(\alpha)`

`t = (5.4)/(0.1886)`

`t = 28.63s`