Question

Plz help me idk what t0o do

Answer 1

`y = - (1)/(2) x + 2`

Explanation:

According to the chart for the values of x (input) the corresponding values of y (output) are given.

The slope of the equation is constant and given by
`m = - (1)/(2)`.

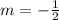If we want to check the slope to be constant then we can use the table and the values of x and y.

The first point (
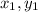`x_(1),y_(1)`) ≡ (-2,3)

The second point (
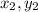`x_(2),y_(2)`) ≡ (8,-2)

The third point (
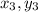`x_(3),y_(3)`) ≡ (10,-3)

The fourth point (
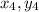`x_(4),y_(4)`) ≡ (20,-8)

Now, we can check that slope of the straight line is constant for all those values.

`(y_(2) - y_(1))/(x_(2) - x_(1)) = (- 2 - 3)/(8 - (- 2)) = - (1)/(2)`

`(y_(3) - y_(2))/(x_(3) - x_(2)) = (- 3 - (- 2))/(10 - 8) = - (1)/(2)`

`(y_(4) - y_(3))/(x_(4) - x_(3)) = (- 8 - (- 3))/(20 - 10) = - (1)/(2)`

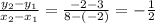
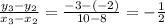
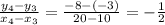
Now, Let us assume that the equation of the straight line is
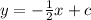`y = - (1)/(2) x + c` ....... (1)

Now, we have to find the value of c.

This straight line passes through (
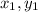`x_(1),y_(1)`) ≡ (-2,3) point.

So, the value of c can be calculated from the equation (1) as, c = 3 - 1 = 2

Therefore,
`y = - (1)/(2) x + 2` is the required equation. (Answer)