Question

Kristin spent $131 on shirts. Fancy shirts cost $41 and plain shirts cost $15. She bought seven

total shirts. How many fancy and plain shirts did Kristin buy?
5 fancy shirts and 2 plain shirts
1 fancy shirts and 6 plain shirts
6 fancy shirts and 1 plain shirts
2 fancy shirts and 5 plain shirts​

Answer 1

1 fancy shirt and 6 plain shirts

Explanation:

We could simply plug in the numbers to figure out the problem.

A. 5 (41) + 2(15) = $235 Incorrect

B. 1(41) + 6(15) = $131 Correct

C. 6(41) + 1(15) = $261 Incorrect

D. (41) + (15) = $157 Incorrect

Answer 2

Kristin bought 1 fancy shirt and 6 plain shirts.

Explanation:

1. Lets name the fancy shirts and the plain shirts as the following:

x = fancy shirts

y = plain shirts

2. The total money spent can be expressed as:

T=x*(cost of fancy shirts)+y*(cost of plain shirts)

As Kristin spent a total of $131 on shirts, where fancy shirts cost $41 and plain shirts cost $15, replacing values we have:

T = (cost of fancy shirts)*x + (cost of plain shirts)*y

131 = 41x + 15y (Eq.1)

3. As the problem says that Kristin bought seven total shirts, the total quantity of fancy and plain shirts can be expressed as:

x + y = 7

Solving for x, we have:

x = 7 - y (Eq.2)

4. Replacing Eq. 2 in Eq. 1 we have the following:

131 = 41(7-y) + 15y

Solving for y:

131 = 287 - 41y + 15y

131 = 287 - 26y

131 - 287 = -26y

-156 = -26y

`(-156)/(-26)=y`

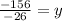
6 = y

And replacing this value in Eq.2 whe have:

x = 7 - 6

x = 1

Therefore Kristin bought 6 plain shirts and 1 fancy shirt.